数字六是中国人都喜欢的吉利数字，也是数学中所谓的“完美数字”的第一个。万众瞩目的中国学子的终极大考--高考从过去的 7 月 7 日提前到了 6 月 7 日，猜想背后也蕴含着人们美好的愿望。在中国，高考是每一年中的一件至关重要的大事，是成千上万的寒窗苦读的学生们迈向自己所憧憬的人生旅程的第一道关口险隘。

各地风雨飘渺的严峻的疫情形势给 2022 年的高考增添了很多的不确定性，但随着高考时间的临近，各地疫情逐渐平复，让家长们感到了一丝丝的欣慰。天气也是出奇地给力，大概从我对高考有印象记忆开始，还没有过这般恰似秋天的凉爽高考天！

高考的第一天下午就是考数学，随着考试结束的铃声响起，考生们神情沮丧地走出考场，家长和老师们迫不及待地上前询问数学考试的战况如何，学生都不约而同地大吐苦水怨声载道，吐槽数学考题真是太难了！线上的视频中还有重点中学的学生难过得掉下了眼泪，可见今年数学考题杀伤力之大，波及四方。

托马斯·贝叶斯（Thomas Bayes，1702-1761），18世纪英国神学家、数学家、数理统计学家和哲学家，概率论理论创始人，贝叶斯统计的创立者，“归纳地”运用数学概率，“从特殊推论一般、从样本推论全体”的第一人。

 P(A|B) = P(A)P(B|A) / P(B)

在上面著名的贝叶斯公式中，P(A)和P(B)都是先验概率，而A有可能是诱发B的一个原因和条件。在观察到事件B发生后对于事件A发生概率的预测是基于原来事件A发生的原始概率预测的一个修正和调整。而这个调整比例P(B|A) / P(B) 被称为似然比。

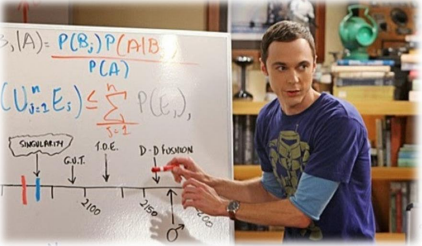
在今年高考数学考卷中赫然发现一道贝叶斯推理计算题：

一个医疗队研究某地的一种地方疾病与当地居民的卫生习惯（卫生习惯分为良好和不够良好两种）的关系，在患该疾病的病例中随机调查了100例（称为病例组），同时在未患有该疾病的人群中随机调查了100人（成为对照组），得到了以下数据：

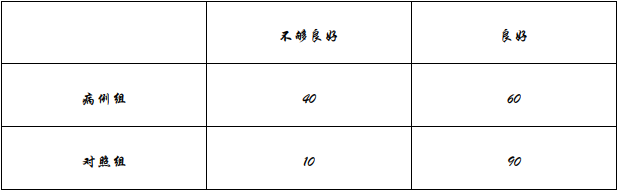
从该地的人群中人选一人，A事件表示“选到的人卫生习惯不够良好”，B 事件表示“选到的人患有该疾病”。A事件表示 “选到的人卫生习惯良好” ，B事件表示 “选到的人未患有该疾病” 。P(B|A)/P(B|A)与P(B|A)/ P(B|A)的比值是卫生习惯不够良好对于患该疾病风险程度的一项度量指标，记为R。

 R = P(A|B)/ P(A|B) * P(A|B)/ P(A|B) 

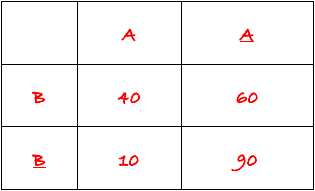
从上面题目所给的数据可以计算出来：

P(A|B)=40/100=0.4;

P(A|B)=10/100=0.1;

p(A|B)=60/100=0.6;

P(A|B)=90/100= 0.9;

R=0.4/0.6*0.9/0.1=6

这道题目很好地揭示了生活中一个非常重要的事实：两个观察到的现象，人们最为关心的就是因果关系，谁是谁的因，谁是谁的果。但是，统计学只能回答相关性而不能回答因果关系。在上面这道高考数学题目中，医学工作者最感兴趣的就是是否不良的生活习惯导致当地人染上这种疾病，第一层思维方式用概率语言来表示就是P(B|A)= P(A|B) * P(B)/P(A)。这就要求人们对于两个先验概率P(B)和P(A)有很好的估计，这两个先验概率的度量都需要大量的样本调查，不仅工作量很繁重，同时统计误差也会非常大。那么就直接导致这样测算的结果 P(B|A)失真严重，所得到的结论也不能被完全相信。

基于以上的原因，直接回答P(B|A)不是一个好的方法。那么退而求其次，第二层的解决方案就在于通过对比具有良好习惯和不具有良好习惯的人群对于这种疾病患病率的影响。注意尽管在第一种方法中，计算的概率P(B|A)本身是一个条件概率，但是，从回答本问题的角度，这个概率是直接的方式。而第二种方法就是以比例 R 的形式出现，R 所度量的就是不良习惯对于患病和非患病人数的比例，再被良好习惯对于患病和非患病人数比例来正规化 Normalize，R是一个被两次正规化的度量，这里最大的优点就是把误差和噪音清除，我们不用再关心先验概率P(B)和P(A)的严谨准确性。 

谈到比例法的清除噪音揭示本质的特点，我给大家提供另外一个我在北大深圳研究院授课时引用的一个有趣例子来诠释： 

假若有两辆汽车，都有安全气囊，一个防死亡率有效性是90%，另一个的有效性是70%，请问这两辆车的安全性是“差不多”吗？ 

在课堂上，大部分学生第一次看到这个问题，不明就里，觉得两种安全气囊的安全防护差不多，一个是90%，一个是70%，伯仲之间。但是，为了看清这个问题的真相，每个人最关心的是气囊没有防住风险，导致死亡的比例。从这个角度上讲：第一种气囊的死亡率是10%，第二种气囊的死亡率是30%，第二种气囊的死亡率是第一种气囊的30%/10%=3倍。孰好孰坏，一目了然。

回到前面讨论的主题，大家可以发现贝叶斯推理的本质就是利用一种可以在生活实践中能清楚观测到的事实和数据来合理地推算某些在实际中很难或者根本不可能观察到的事实，这里面有很多是人们所向往的因果猜测！ 

在上面高考数学题中，P(A|B)是可以直接观测到的统计数据，而相反，P(B|A)是无法直接观察到的。因果关系的度量指标R最终是通过贝叶斯公式的神奇转换，里面的参数都被可以直接观察到的统计数据所替代，这就是数学之美数学的伟大。它能帮助人类顺利完成了因果关系推导的不可能之任务。

我去年在疫情隔离期间无意中看到了一位同样以概率思维为主线的教育工作者老喻的文章，开始关注他的动向。在最近的一篇文章中，老喻提出了一个非常耐人寻味的有趣问题，也是他在加拿大家里的真实经历。我就用这个生动的例子来进一步说明伟大的贝叶斯推理在日常生活中如何提升人的深层认知能力，指导人们做出正确（有时候是艰难）的抉择。 

假设一户人家，男主人外出，突然接到家里的电话说是家里的爱犬金毛找不到了，男主人在安慰了家中的妻子和孩子之后，冷静地根据历史大数据做了如下的基本假设：金毛有

90%的概率在后院 

7%的概率跑出后院到了森林 

3%的概率被人偷走

男主人告诉家人在家里和后院仔细寻找，家人在后院找了一圈，没有找到金毛，又再次焦急地打电话告诉男主人，问下一步如何寻找？假设在后院找过金毛但没找到的概率是 10%，假设事件 A代表金毛还在后院，事件 B 代表在后院找了金毛，但没有找到。 

那么，P(A)= 90%；P(A) = 10%。

利用贝叶斯推理的语言，这些都是通过历史大数据总结的先验概率。

根据已知条件，金毛还在后院，但没有找到的概率很小，只有10%，用概率来表示就是P(B|A)=10%, 现在真正挑战的是要计算出逆概率P(A|B)的大小，而P(A|B)所代表正是，已经在后院找过了没有找到金毛，问在这种条件下，金毛还在后院的概率可能性。

注意，在上面的计算中，P(B|A)=100%，是因为事件A代表金毛不在后院，那么肯定是找不到它的！ 

基于上面的计算，大家可以看到，即使第一次在后院寻找金毛，没有找到，它还在后院的概率竟然还有近乎一半的概率可能性，远远大于另外两种选择7%和3%的概率！ 

根据老喻的亲述，他就是经过上面的考量，再次打电话通知家人再到后院仔细找一次。家人们非常仔细把整个后院进行了地毯式搜索，四处大声呼唤金毛的名字，突然听到了悉悉索索的声音，在后院Deck地毯下的一个隐藏的洞里发现了浑身是土惊慌失措的金毛，大家喜出望外地把它从洞中救了出来，贝叶斯推理救了金毛一命！ 

这个例子像极了发生在1968年的美国海军天蝎号核潜艇在大西洋亚速海海域失踪事件，潜艇和艇上的99名海军官兵全部杳无音信……事后调查残骸发现，罪魁祸首竟是潜艇自己发射的鱼雷击中了自己，多么不可思议！

美国海军在茫茫的大西洋中苦苦搜寻了几个月，一无所获，只能求助于美国海军的首席科学家John Craven，John不紧不慢地拿出一张标注着不同颜色的海洋地图：

他又在白板上写出来两个数学公式：

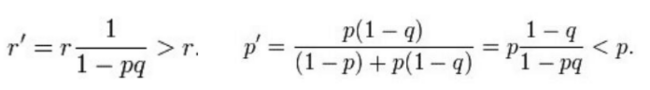
John把核潜艇沉没的区域划分成很多同样大小的正方形，图中每个格子所在的海域是考虑到鱼雷冲击波，水流等因素后潜艇残骸可能散落的区域，p和q分别代表残骸散落到某个格子的概率以及在该格子内能够被找出来的概率，不一定核潜艇在某个格子就一定能被找出来，这和海域深度有关系。 

假设核潜艇在这个格子里的先验概率为p= P(A)，潜艇在这个格子里，搜寻后发现潜艇的概率为q=P(B|A)，则类似于上面寻找金毛的问题，搜寻后没有发现潜艇，但潜艇还是在该格子里的后验概率，利用贝叶斯公式是：

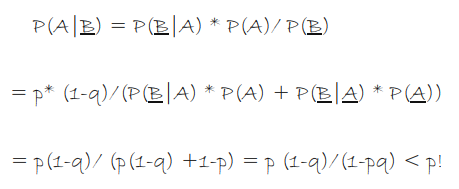
相反，对于另外的格子里找到核潜艇的概率，在得知在当前的格子中没有发现潜艇的事实更新下，有以下的变化和调整：

也就是说每次搜寻完一个格子后，潜艇残骸在这个格子里的概率p'就比之前p下降了；而同时，残骸在其它格子的概率就会上升。所以，完成一次搜寻，全部区域都会重新洗牌，每次都会生成一个概率最大的格子，搜寻几次后某个格子的概率就会特别大，美军每次都驶向那个贝叶斯概率最大的方格，就真的很快找到沉没的核潜艇。 

概率论中古老的贝叶斯推理竟然在 20 世纪帮助人类完成了一个几乎是不可能的任务，再建新功。

贝叶斯推理不仅在日常的工作生活中为我们做出正确的决定提供了一个严谨的思维框架，同样的，它也在企业管理和规划中大显身手。随着企业数字化的推广，数字化技术不仅改变了下层的业务运营模式，更重要的是启迪企业家运用更加科学的数字化思维来为企业未来的发展做决策，情景分析压力测试等方法都被引入到了董事会的战略分析中。

一种经典的场景就是企业面临一个未来业务的决策，在做战略分析研判的时候，董事会会引入未来不同的经济场景，计算核查该项业务在不同场景下的得失和损益。

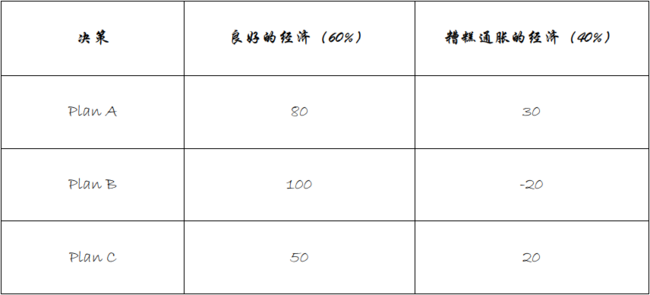
三种计划的预期值计算出来是：

E(Plan A)=0.6*80+0.4*30=60（最佳） 

E(Plan B)=0.6*100+0.4*(-20)=52 

E(Plan C)=0.6*50+0.4*20=38 

这里的经济好坏的概率都是先验概率，总结历史上的大数据得出的结论。但是，没有人能未卜先知，知道未来的经济状况的好坏，为数不多的信息来源就是求助于经济学家的报告和预测。假设，利用历史大数据统计得出结论：在经济状况好的的时候，经济学家有80%的概率得出正确的预判，有20%的概率做出错误的判断。在经济状况不好的时候，有90%的概率预判正确，有10%的概率过于乐观得出错误的结论。把这些条件写成条件概率，就得到了下表：

假设经济学家发布了正向的经济报告，那么 

P(好经济|正向报告)

=P(正向报告|好经济)* P(好经济)/P(正向报告) 

= P(正向报告|好经济)* P(好经济)/(P(正向报告|好经济)*P(好经济)+P(正向报告|不好经济 )*P(不好经济)） 

=0.8*0.6/(0.8*0.6+0.1*0.4)=12/13=92.3%

同样的，P(不好经济|正向报告) 

=P(正向报告|不好经济)*P(不好经济)/P(正向报告) 

=P(正向报告|不好经济)*P(不好经济)/(P(正向报告|好经济)* P(好经济)+P(正向报告|不好经济)*P(不好经济))

=0.1*0.4/(0.8*0.6+0.1*0.4)=1/13=1-92.3% = 7.7%

在更新的概率下，重新计算三种不同方案的预期值： 

E(Plan A)=0.923*80+0.077*30=76.15 

E(Plan B)=0.923*100+0.077*(-20)=90.76 （最佳） 

E(Plan C)=0.923*50+0.077*20=47.69 

概率思维是一种世界观，统计思维是一种认识世界的方法论。有用的贝叶斯推理，人人都值得拥有。

（文章版权归作者所有）