HKU ICB
陆晨博士:疫情中的数学 | 深度观点
Back11 Apr 2022 | 财务金融

人类一切的智慧都包含在这四个字里面:等待和希望。——大仲马
序言
伴随着这场艰苦卓绝的全球性抗击疫情的世界大战进入了第三年,人们不约而同地期待着战胜新冠病毒疫情的日子为期不远了。尽管各国防疫政策和管理措施千差万别,但是,人类向往美好健康正常生活的渴望是完全一致的,人性使然也。
抗击疫情的过程中,新冠病毒不断变换攻击人类的方式从第一代在武汉发现的杀伤力极强,危险性很大的病毒,演变到Delta,再变化到令世界各国谈毒变色传染力大杀四方的Omicron,人类也在变化和不确定性中不断审视调整自己的防疫战术和应对方法。中国各地政府在党中央的领导下以“动态清零”为指导方针,医护和基层工作人员不眠不休忘我地工作,被老百姓誉为新时代“最可爱的人”。
对抗新冠疫情的战役进行到了2022年,疫情在各地又是狼烟四起,多个前两年防范疫情的模范标兵:上海深圳天津都不幸地相继“失陷”。但是我们的有效防护办法还只是注射疫苗和隔离。由此,几乎每个人的家庭成员亲朋好友同事或者本人都有着隔离的不同经历。
我在2021年圣诞节的时候到上海陆家嘴给香港大学SPACE中国商学院授课,所住的凯宾斯基大酒店因为一位无症状感染者的入住,导致我被视为和这位从未谋面的病毒携带者有着“时空交错”(很像量子力学中的术语),无比高效的流调就让我开始了2022年开年不久的第一场隔离,而完全没有想到的是,当我完成了政府要求的隔离,一踏出隔离酒店,迎来的却是家乡铺天盖地的国内首批Omicron疫情的来临。大街上空无一人,每个小区和街道都剑拔弩张,严阵以待开始了疫情中首次的大规模核酸检测。
新年将至,看到家乡的疫情来势汹汹,我就想要赶紧离开奔赴深圳回香港。但是,因为拿不到政府要求的离津证明没能成行。现在大家都看到了,香港成了一个疫情高发地,每天几万人,大陆也派了医疗团队赶过去帮助香港政府抗击疫情。由此我再次深深地感受到了世事的不可预测性,暗中庆幸自己阴错阳差地躲过一劫,没有回香港。
妈妈接被隔离孩子的概率问题
尽管自2020年从香港回到大陆开始第一次隔离开始,我已经历了数次集中隔离的挑战,但由于过去做华尔街交易员的缘故,我的心理素质超级过硬,还有另外一个方面就是作为曾经的“数学家”,对于孤独寂寞的忍受能力易于凡人,所以,我并不感到隔离会对我有什么负面的影响(每天都坚持不懈地健身)。唯一不足就是视觉空间的索然无味,不经意间,我发现重拾我的老本行深度思考挑战性极强的数学问题会把我从这个固定有限的物理空间中拯救出来,带到了另一个无比广阔深邃虚幻的数字世界,在那里,我不再受地域的限制,可以让发散思维带着我随心所欲的翱翔。
大家听起来是不是颇有今年年初风靡一时的元宇宙的味道,从现实物理空间升华到另一个宇宙维度。数学的魔力就在于把人从痛苦复杂的现实中解脱出来,沉浸于纯粹圣洁优美的数学世界里发现更多妙不可言的数学之美,数学是上帝的语言和福音,它给人类带来的是绝对的真实和深刻。当我被自己的思想所引领,进入到这个神奇缥缈的世界中,物理世界中的烦恼和痛苦都不复存在了。
每一轮病毒都有着它自己迥然不同的“口味”,Omicron病毒对于年幼的孩子和学生群体情有独钟,很多地方的学校孩子感染的概率不断增大(现在吉林省面对的就是这个棘手的问题)。于是人们不断地在微信或者短视频平台上看到一幕幕催人泪下的场景,一个个穿着硕大无比防护服的孩子喊着“爸爸”、“妈妈”,步履踉跄地被防护人员带走去做集中隔离,2022年的疫情注定在这些幼小的心灵和记忆中留下终身难忘的一笔。
和疫情中孩子们隔离相关的一个有趣的数学概率问题,孩子们被带走顺利地完成了集中隔离,安全无恙地返回,家长们急不可待地赶过来把自己的孩子领回去,但是,就像下面图中所显示的,孩子们都穿着统一的防护服就像一个个可爱的小太空人,家长们很难辨别哪一个是自家的孩子,所以,能够想见,领错孩子是很容易发生的。那么一个有趣的问题就是:n个孩子都穿着整齐划一的防护服,n个妈妈来接孩子,请问每个妈妈都接错自己孩子的概率可能性有多大?

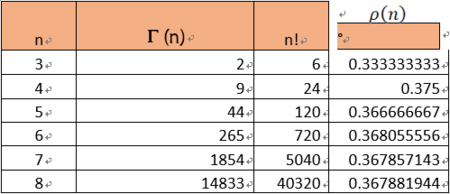
用Γ(n)来表示n个妈妈都没有接到自己孩子的可能性,简单起见,我们列出初始的几个n值下Γ(n)是多少:Γ(1) = 0,Γ(2) = 1, Γ(3) = 2,Γ(4) = 9,Γ(5) = 44,Γ(6) = 265 , Γ(7) = 1854 ;Γ(8) = 14833。
对于一般性的情况,可以发现 Γ(n) 就是要在全部n!的排列中排除掉只有一个妈妈接到孩子、只有两个妈妈接到孩子、只有三个妈妈接到孩子,以此类推
Γ(n) = n!- C(n,1) * Γ(n-1) - C(n,2) * Γ(n-2)-C(n,3) * Γ(n-3)-……-C (n, n- 2) × Γ(2)-1
那么,n个妈妈都接不到自己孩子的概率就是 Γ(n) / n!
我们记这个概率为 , 则上面的等式就变为
= 1 - C(n,1) * Γ(n-1)/ n! - C(n,2) * Γ(n-2)/ n! -- C(n,3) * Γ(n-3)/ n! - …… - C (n, n-2) * Γ(2)/ n! - 1 / n!
= 1 - C(n,1)/n * Γ(n-1)/(n-1)! - C(n,2)/n(n-1) * Γ(n-2)/ (n-2)! - C(n,3) /n(n-1)(n-2)* Γ(n-2)/ (n-2)! …… - C (n, n-2)/(n(n-1) ……3) * Γ(2)/ 2! - 1 / n! ( * )
注意到 C (n, k)/(n(n-1) ……(n-k+1)) = 1/ k!
=1–1/1!–1/2!–1/3!…… - 1/(n-2)! - 1 / n! (**)
+ 1/1! + 1/2! + 1/3!…… + 1/(n-2)! + 1 / n! =1
假设:当n趋向于+∞,极限存在,为 A,就有(忽略前面有限项的不同值)
A + 1/1!A + 1/2!+ 1/3!…… + 1/(n-2)! + 1 / n! A +…… =1
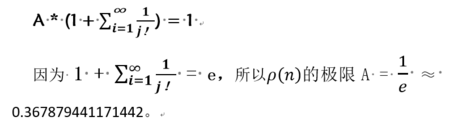
在这里必须说明的一点就是,上面导出结论的部分更像是物理学家的处理方式,从数学家的角度需要从递归公式(**),证明这个序列p(n)柯西收敛,技术细节就不一一列出了。

综合上述,当孩子很多的时候,每个妈妈都领不到自己孩子的概率是1/e。这里特别说明一下,e这个神奇的常数叫自然常数,因为它和人类生活的物理世界的方方面面都有着重要的联系,选用字母e来代表自然常数是来纪念的它的发现者瑞士伟大多产的数学家欧拉Euler。
核酸检测和信息论
新冠病毒疫情彻底地改变了人们的生活方式,现在戴口罩测核酸成为每个在大都市拼搏的人生活中必不可少的重要组成。随着2022年初疫情在全国范围内不断蔓延,各个地方对于核酸检测的要求也是不断加强和完善,深圳上海都是每48小时要测一次核酸。人们也在不断摸索检测核酸的方式,使之更加高效和便捷。
一个新的核酸检测方式就是混检,10个人,20个人一组来测核酸,这其中的道理很简单,大部分都是健康的阴性,核酸阳性的病毒携带者在中国大陆是少数,核酸混检可以大大降低核酸检测成本,提升检测效率,缩短检测时间。
一旦发现一个混检样本为阳性,就要重新召回这一组的人来筛查,最简单粗暴的方法就是每个人需要再单独检测一遍,就能准确无误地发现谁是阳性感染者。
如果一组10个人做核酸混检,发现结果为阳性,那么从节约成本的角度,最少测几次就能找出新冠病毒携带者呢?注意,这一组人中,有可能一个或者多个人是阳性。这是一个很实际也很有趣的问题。
如果就像现在实际中所呈现的统计比例,核酸检测为阳性的人比例很小,10个人中有1个阳性,则最有效的方式就是通过二分法来剥离筛选出来。
先把10个样本分成两组,随机选取5个样本为第一组做一次混检,无论结果如何,都能锁定阳性是在哪一组的5个人中。下一步,把5个样本随机分选3个做混检,如果是阴性,则阳性患者肯定在余下的两人中,随机选择一个样本做检验,就会锁定最后的目标;如果3人组的检测结果是阳性,则还需要2次发现阳性病人。按照这样的步骤,找到10个样本中唯一的阳性需要3次到4次,相比核酸单检的10次,效率提高了很多。
上面所讨论的其实都属于由AT&T的著名科学家Claude Shannon香农所创立的信息论范畴。创立信息论这一点被另一位发明控制论Cybernetics的MIT著名数学家Norbert Wiener所反对挑战,认为Shannon剽窃了自己的创新想法。
一个事件X°=x的°自信息 (self-information)°
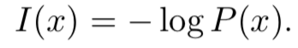
在信息论里则叫信息量,这里的对数有两种选择方式,如果选在上一章节中出现的神奇自然数e,定义的I(x)°单位就是奈特(nats)。一奈特是以1/e(计算出来的每个妈妈都接错自己孩子的概率!)的概率观测到一个事件时获得的信息量。另一种选择是使用底数为2的对数,单位是比特(bit),当A发生的概率正好是1/2时,需要的信息熵达到顶峰,是1比特Bit。比特币BitCoin的比特就是来源于此。通过比特度量的信息是通过奈特度量信息的常数倍。Shannon借鉴19世纪热力学和统计力学的熵公式,提出了著名的信息熵概念和公式:
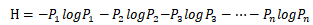
从Shannon的信息论的角度,10个样本中有一个阳性,则总体的不确定性为、log(10)。每次做核酸检测,只有两种结果 阴性和阳性,所以可以消除的信息量为log(2)。那么,需要做log(10)/log(2)= 3.32次,这和我们前面提供的操作算法是相符的。
如果已知10个人中有2个阳性,那么总体的不确定性为log(C(10,2)),需要至少做log(45)/log(2)= 5.49 次。以此类推,3个阳性就需要log(120)/log(2) = 6.9,4个阳性竟然需要log(210)/log(2)=7.71次。
由此可见,随着可能的阳性病人的数量的增加,需要做核酸检测的最少次数快速趋近于10次,也就说是对于每个核酸样本进行单独检测是最有效的解决方案。
在实际的检验中,核酸样本中有多少个阳性病人是不知道的,当然,从大数据统计的方面,可以依据前期所采集检验的核酸样本的阳性比例作为一个指导标准来很聪明地猜一下。假设我们对此一无所知,可以用一个简单的“投机”算法,把10个样本分为两组分别做一次集体核酸检测,只有两种结果:
A) 有一组为阴性,一组阳性
B) 两组都为阳性
阴性的样本可以剔除,对于任何一组是阳性的,就马上开始对组内每一个样本做单独检测,逐一排查,发现真相。
一个信息论中很有趣的著名例子就是小球问题:有12个小球,其中有一只小球和其他小球都不同,但不知道这个特殊的小球是比其他的小球是轻还是重,请问用一架天平称重几次能找出这只有瑕疵的小球?
利用Shannon信息熵理论,有log(12*2)/log(3)= 2.89,所以,最少是要称重3次来找到那只与众不同的小球。
把12只小球分为3组:I(a,b,c,d), II(e,f,g,h), III(i,j,k,l),进行第一次称重
a b c d 和 e f g h,如果它们一样重,那么有瑕疵的小球肯定就在余下的 i j k l 中。
做第二次称重 i j 和 a k ,如果天平平衡,则知道小球 l 有问题,最后一次用已知的正常小球 a 和 l 称一下就真相大白了。
如果天平不平衡,不失一般性,假设 i j < a k, 则再称一次 i 和 j,如果是同样重,则必定有 k 是一只重的小球;反之,如果是i 和 j 不一样重,那么那个轻的就是有问题的小球。
如果 a b c d 和 e f g h不一样重,不失一般性,假设 abcd < efgh。则可知,余下的ijkl都是没有任何问题的小球,则做如下的称重abe 和cfi。
如果abe = cfi,一样重,那么,有问题的小球只可能在d或者gh中,要么d是轻的小球或者gh中有一个是重的小球。最后只需要测一次g和h,一切就水落石出了,因为如果它们一样重,则d就是要找的轻小球。如果g和h不一样重,则重一些的那一只就是要找的。
如果abe < cfi, 则小球c d e g h都是没有问题的(想一想,为什么小球c和e都是好的?),只可能 ab中有一个轻的小球或者f是一个重的小球。最后一次,只需要称重a和b,如果同样重,则f就是重一些的小球;否则ab称重中较轻的那一只就是我们要找的。
如果abe > cfi,同样得出结论小球c d e g h都是没有问题的,只可能ab中有一个重的小球或者f是一个轻的小球。最后一次,只要来用天平称重a和b,相同重量,则f是那只轻的小球。如果a和b重量不同,则重的那一只就是最后的答案。
(版权归作者所有)